Teoria delle antenne

 |
FREQUENZA E LUNGHEZZA D'ONDA Qualsiasi onda radio ha due componenti:la corrente e la tensione che variano il loro valore nel tempo secondo la velocità della luce ( circa 300.000 km/s ) assumendo una forma sinusoidale della figura 1 che, per semplicità, rappresenta il valore delle tensione. Nel punto A essa ha valore zero mentre nel punto B ( picco ) assume un valore massimo positivo. Successivamente il valore diminuisce fino ad annullarsi nel punto C per poi raggiungere un picco negativo in D. La distanza tra due punti dell’onda aventi lo stesso valore, ad esempio tra i punti A ed E oppure B F, si chiama PERIODO o CICLO. Il numero di cicli che un’onda compie in un secondo si definisce FREQUENZA ( F ) e si misura in Hertz ( simbolo Hz). Il rapporto che intercorre tra la velocità dell’onda ( quella della luce ) e la sua frequenza definisce la LUNGHEZZA D'ONDA ( LO ) e si esprime in metri ( m ) secondo la formula: 300000 LO = ----------- F Nella quale F si esprimerà in chilohertz (kHz). Ad esempio: per una frequenza pari a 6000 la lunghezza d’onda sarà di 50 m. 300000 LO = ---------- = 50 m 6000 FREQUENZA DI RISONANZA L’efficienza di un’antenna è importante per assicurarsi ottimale ricetrasmissione. I radioamatori americani sono soliti affermare: “ Spendi un centesimo per l’apparecchio e 1000 dollari per l’antenna “. Nella figura 3 sono rappresentate due corde metalliche aventi le stesse caratteristiche meccaniche e ugualmente tese. Facendo vibrare una delle due, l’altra, seppur distante fino a 3 centimetri vibrerà autonomamente: esse sono in risonanza cioè oscillano sulla stessa frequenza. Il fenomeno suddetto si puo’ estendere alla radiotecnica: un filo metallico di lunghezza casuale è capace di ricevere onde radio qualsiasi valore di frequenza ma solo uno sarà ricevuto in modo ottimale. Esisterà cioè una risonanza tra il valore della frequenza del segnale radio ricevuto e le caratteristiche fisico-meccaniche del filo che costituisce l’antenna: la FREQUENZA DI RISONANZA. Apparentemente un filo metallico ( Fig. 2 ) sembra perfettamente rettilineo; in effetti, però, le piccolissime ondulazioni di cui è composto fanno somigliare il filo ad un solenoide e introducono, oltre alla resistenza R intrinseca, anche un’induttanza ( L ) ed una capacità ( C ). Se il filo in questione viene investito da un segnale radio ( quindi variabile sinusoidalmente i parametri L e C genereranno due valori specifici: XL = 2 * 3,14 * F * L REATTANZA INDUTTIVA XC = 2 * 3,14 * F * C REATTANZA CAPACITIVA Nelle due formule il valore F è quello della frequenza del segnale radio ricevuto. Le due reattanze si misurano in Ohm. Le reattanze, assieme alla resistenza caratteristica, definisce l’IMPEDENZA CARATTERISTICA DI UN’ANTENNA ( Z ) calcolabile con la formula: Z = R + ( XL + XC ) Considerato quanto scritto fino ad ora si intuisce che ogni antenna, proprio per la differenza di configurazione fisico-meccanica, possiede un valore caratteristico di impedenza. Un dipolo a mezz’onda presenta una Z caratteristica di 70 Ω mentre un dipolo ripiegato possiede una Z di 300 Ω. TRASFERIMENTO DEL SEGNALE Anche il collegamento dell’antenna all’apparecchio ricetrasmittente non puo’ essere casuale. Una volta scelta l’antenna da usare occorrerà trasferire il segnale dall’apparato usando una linea di alimentazione adeguata. Anche i cavi coassiali impiegati nelle comunicazioni hanno impedenze caratteristiche. Un cavo RG-58 o RG-8 presentano una Z caratteristica di 50 Ω. Però non potremo alimentare un’antenna tagliandolo a casaccio bensì con cognizione di causa. Supponendo che la nostra antenna abbia una Z di 100 Ω e che disponiamo solo di un cavo di tipo RG-8. Se useremo il cavo tagliato a ½ λ uno strumento ( impedenzimetro ) posto invece dell’antenna misurerebbe il valore di 100 Ω. La figura 4 e la tabella daranno indicazioni chiare. Per esempio: un’antenna GP con impedenza caratteristiche di 50 Ω dovrà essere collegata all’apparecchio radio con uno spezzone di filo coassiale RG-8 tagliato a ½ λ della frequenza di risonanza oppure a λ intera o a multipli di ½ λ. |
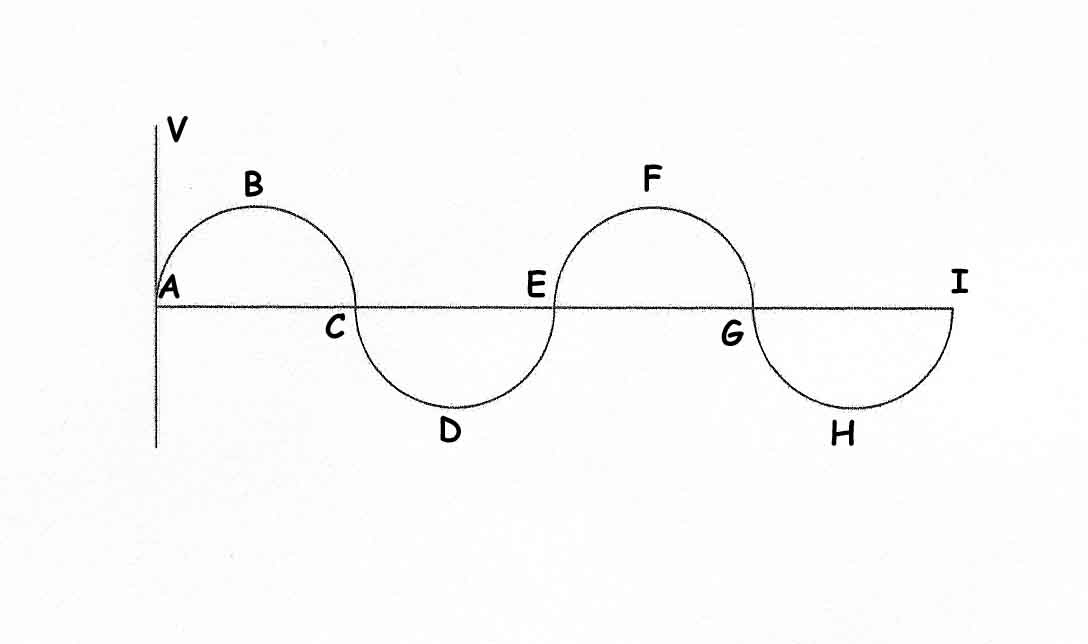 Fig. 1 |
|
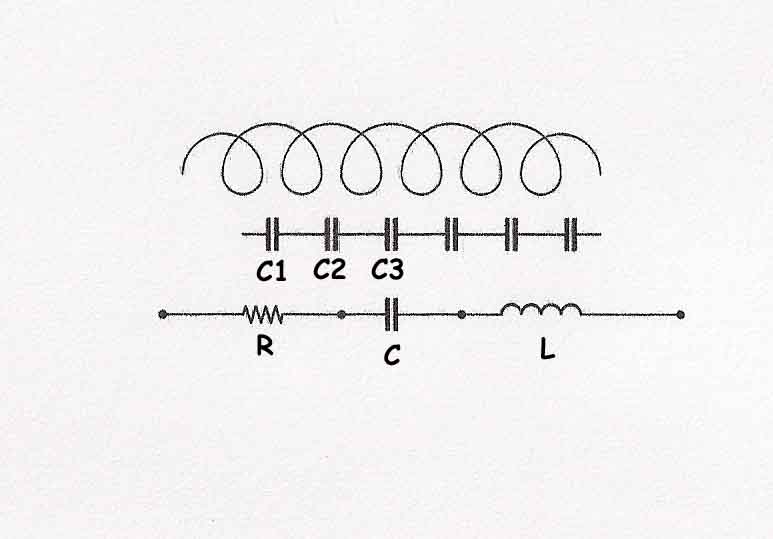 Fig. 2 |
|
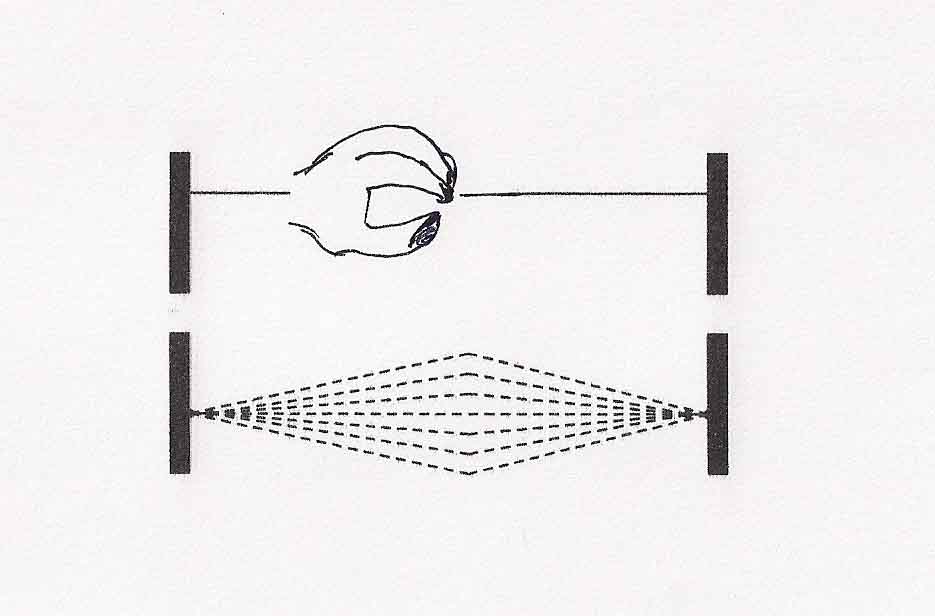 Fig. 3 |
|
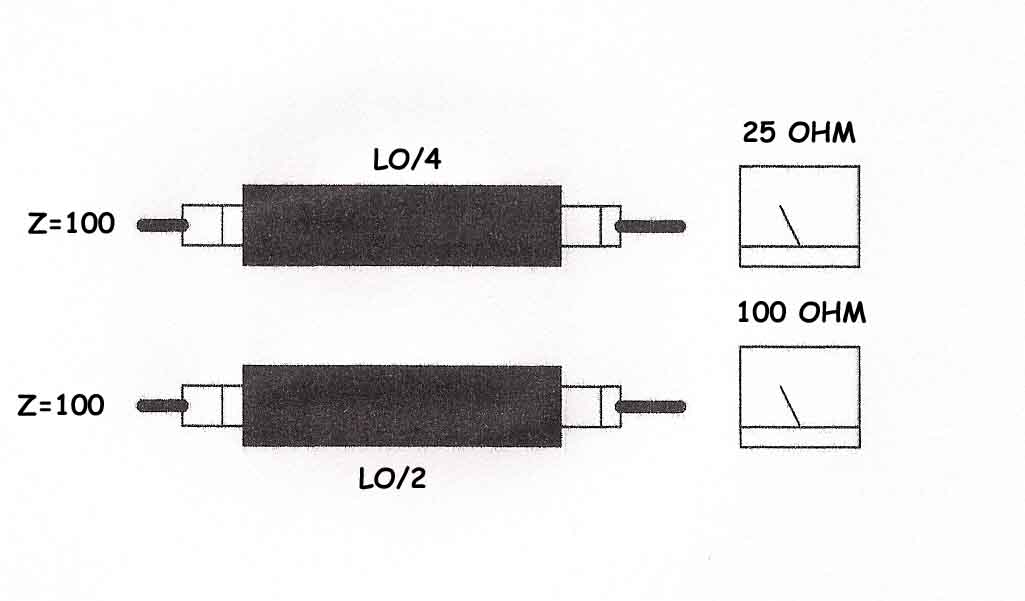 Fig. 4 |
|
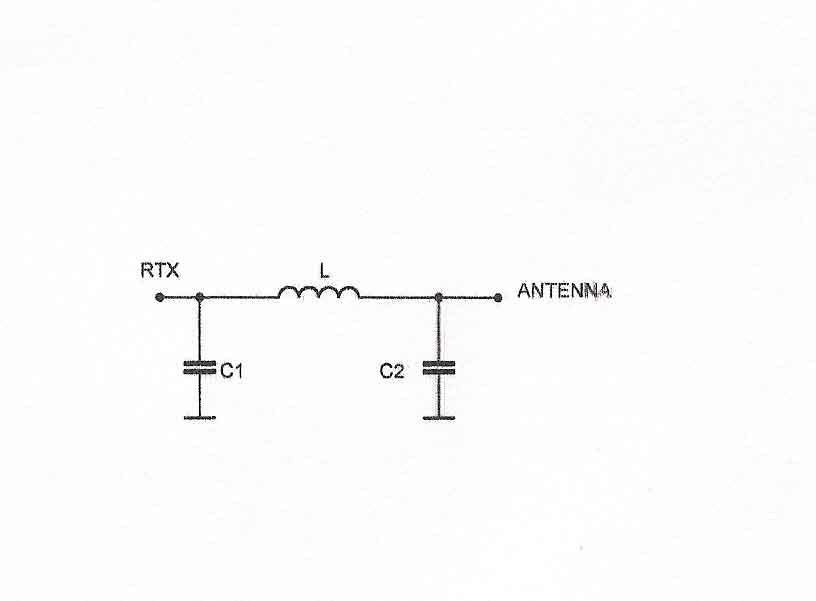 Fig. 5 |
|
|
In conto dovremo mettere, variando la lunghezza del cavo
coassiale, la dovuta attenuazione del segnale e, naturalmente,
il costo maggiore. QUALE ANTENNA? Agli albori del radiantismo le uscite per le antenne degli apparecchi avevano la possibilità di adattarsi all’antenna usata. In genere l’ultimo stadio degli apparecchi ricetrasmittenti aveva un circuito configurato a Π greco con uno schema elettrico come illustrato in figura 5. La tecnica moderna ha uniformato le uscite su un valore standard di 50 Ω anche se gli apparati, con un sistema elettrico particolare, possono accogliere antenne con Z caratteristica dal valore variabile da 30 a 150 Ω. Un sistema APPARATO-LINEA-ANTENNA efficiente e dalle minime perdite è basilare sia per l’attività radioamatoriale che per quella del broadcasting listening. Ecco perché non bisogna trascurare questo aspetto anche se, molte volte, le condizioni logistiche in cui si opera lasciano poco spazio all’osservanza pedissequa della teoria. Come vedremo, bisognerà venire a compromessi. Se per un radioamatore la soluzione è semplice ( un’antenna dimensionata per i 7 MHz risuonerà, bene o male, anche sulle frequenze armoniche ) per un BCL-SWL le cose sono più complesse dato l’ampio spettro di frequenze da ricevere. Per quest’ultimi sarebbe ottimale un parco antenne composto da una cortina di dipoli accordati sui centro gamma e accontentarsi di ricevere le frequenze adiacenti con minore rendimento. Però in questo caso il problema dello spazio prevale su tutta la questione. |
|


